문제링크

2749 - 피보나치3

문제

입력

첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.

풀이 유형

다이나믹 프로그래밍
수학

풀이

n이 상당히 크다. O(n)만 해도 시간 내에 풀 수 없는 문제다. 즉, O(log n)의 시간복잡도 내에 해당 문제를 풀어야 한다. 수학 문제인만큼 풀이는 간단하다.

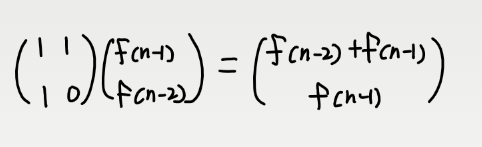
위의 행렬식을 생각해보면, 조금 더 쉽다. 앞에 곱한 행렬을 거듭 곱해주면 자연스럽게 피보나치의 차수가 올라간다. 해당 행렬의 거듭 곱은 그냥 무식하게 n번 곱하는 것이 아니라 log 2번 만에 곱할 수 있다. 거듭 제곱을 분할 정복으로 하는 방법은 간단하다.

1
2
3
4
5
6

def pow(n, k) :
    if k == 1 :
        return n
    if k == 0 :
        return 1
    return pow(n, k/2) * pow(n, k/2) * pow(n, k%2)

이제 어떤 느낌인지 대략 감이 올 것이다. 행렬곱을 거듭제곱 즉 분할정복을 통해 여러번 곱해주면 되는 것이다. n번째 숫자를 찾는다면,n/2, n/4, n/8…etc..
아래는 피보나치의 규칙성을 식으로 나타낸 것이다. 필자는 아래의 방법을 사용했다. 메모이제이션을 통해, 동적 계획법의 관점에서 접근을 하고자 했다. 단위가 너무 크기 때문에 해쉬함수를 사용했다.

1

fib(n) = fib(k+1)*fib(n-k) + f(k)*fiv(n-k-1)

행렬을 직접 구현해서 곱해도 좋고, 위의 식대로 풀어도 좋다. 이 방법 이외에 피사노 주기를 이용하여 푸는 방법이 있는데, 모듈러 연산이라는 점을 이용하여 풀이하는 방법이다. 사전 지식이 필요한 만큼 나는 그다지 선호하는 풀이는 아니기에 기술하지 않겠다.

마무리

손으로 직접 쓰다보면, 피보나치의 점화식을 늘리는 대신 연산 횟수를 확실히 줄일 수 있다. 수학 문제가 풀리지 않을 때는 열심히 적어 보자.

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

#include <iostream>
#include <map>

#define mod 1000000

using namespace std;
long long int N;
map<long long int, long long int> dp;

long long int fib(long long int n){
    if(n <= 0) return 0;
    if(n == 1) return 1;
    if(n == 2) return 1;
    if(dp.find(n)!=dp.end()){
        return dp[n];
    }
    long long int k = n/2;
    dp[n] =  (fib(k+1)*fib(n-k) + fib(k)*fib(n-k-1))%mod;
    return dp[n];
}

int main(void){
    ios::sync_with_stdio(false); cin.tie(NULL);
    cin>>N;
    cout<<fib(N)<<endl;
}