문제링크
문제
성대나라에는 각 도시별로 가뭄을 대비하기 위한 물탱크가 하나씩 존재한다. 이 물탱크들은 모두 연결되어있으며, 루트(성대나라의 수도)가 있는 트리의 형태를 가진다.
지금 성대나라는 물탱크의 물을 사용하여 가뭄을 버텨냈으나, 그 영향으로 모든 물탱크에 물이 비어버리고 말았다.
성대나라의 물관리 시스템은 다소 특수해서, 물은 항상 다음과 같은 방식으로 채워진다:
A번 도시에 물을 채우기로 했다면, 수도에서부터 A번 도시까지 잇는 직선 경로에
수도부터 차례대로 1L, 2L, ⋯이 채워져서 A번 도시에는 (수도부터 A번 도시까지의 도시 수) L 만큼 추가된다.
예를 들어, 아래 그림과 같이 물탱크가 연결되어 있을 때, "4번 도시에 물을 채운다"라고 하면, 1번 도시에 1L, 4번 도시에 2L의 물이 추가된다. 만약 "5번 도시에 물을 채운다"라고 하면 1번 도시에 1L, 2번 도시에 2L, 5번 도시에 3L의 물이 추가된다.
성대나라의 물탱크 관리 담당인 균관이는 어느 도시에 몇 리터의 물이 저장되어있는지 자신이 궁금해질 때마다 알기를 원한다. 균관이를 도와주는 프로그램을 만들어보자.
입력
첫째 줄에 성대나라의 도시의 수 N (1 ≤ N ≤ 200,000)과 수도의 번호 C (1 ≤ C ≤ N)가 공백으로 구분되어 주어진다.
둘째 줄부터 N-1개의 줄에 연결되어있는 두 도시의 번호 쌍 x, y가 공백으로 구분되어 주어진다(1 ≤ x, y ≤ N, x ≠ y). 물탱크의 연결 형태는 트리 구조임이 보장된다. N+1번째 줄에 질의의 수 Q(1 ≤ Q ≤ 200,000)가 주어진다. N+2번째 줄부터 Q개의 줄에 질의가 들어온다. 질의는 다음과 같이 두 종류 중 하나로 주어진다:
- 1 A : A도시에 물을 채운다.
- 2 A : 현재 A도시에 얼마만큼의 물이 채워져 있는지 출력하라.
두 경우 모두 1 ≤ A ≤ N 을 만족한다.
풀이 유형
풀이
우선, n번 노드에 차 있는 물은 n번 노드를 포함한, n번 노드의 하위 노드들을 모두 합한 것에 깊이를 곱한 값이 된다. 왜냐하면 루트에서 시작하면, n번 노드에 부어지는 물의 양은 n번 노드의 깊이로 항상 일정하기 때문이다. 그렇게 생각하면 이 문제는 구간합 문제로 치환될 가능성이 보인다. 처음의 인풋은 비록 노드의 순서가 뒤죽박죽이지만, 새로이 인덱싱을 해준다면 하위 노드들이 연속된 인덱스를 갖도록 할 수 있는 것이다.
즉, 트리의 인덱스를 새롭게 할당한다. dfs를 통해 거쳐가는 순서가 곧 노드의 index가 된다. 또한 그것을 이용하여 인덱스 트리를 작성한다. 인덱스 트리란, 자신의 하위 노드들의 최저 인덱스와 최고 인덱스를 상위 노드에 기억시켜둔 트리를 의미한다.
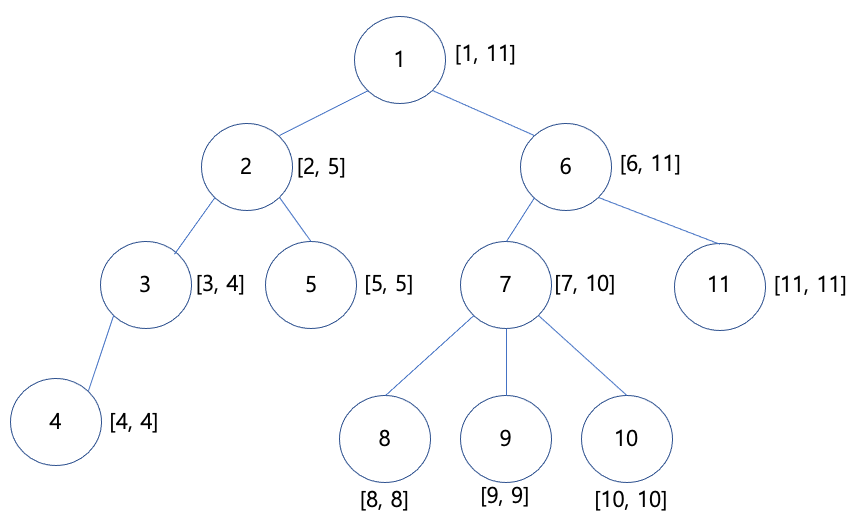
위 사진을 참고하면 편할 것이다. 기존의 인덱스를 위의 인덱스 처럼 다시 바꾸고 나면, 이제 이 문제의 풀이가 가닥이 잡힌다. 상위 노드는 하위 노드의 인덱스 영역을 알고 있다. 즉, 우리는 하위 노드의 인덱스 범위의 구간합을 해주어야 하는 것이다. 이는 세그먼트 트리를 통해 O(log n)의 시간에 처리될 수 있다.
업데이트도 O(log n), 파인드도 O(log n)으로 가능하므로, 쿼리의 수 m에 대하여 해당 알고리즘의 시간복잡도는 O(m log n) 이 된다.
마무리
구간합 문제라는 생각이 드는 순간부터는 술술 풀리지만, 거기까지 생각하기가 어렵다. integer 범위가 넘어갈 수도 있으므로, 자료형에 주의 하자.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
#include <algorithm>
#include <stack>
#include <map>
#include <cmath>
#define Min(X, Y) ((X) < (Y) ? (X) : (Y))
#define Max(X, Y) ((X) > (Y) ? (X) : (Y))
typedef long long int ll;
using namespace std;
int N, C, NodeNum = 0;
vector<int> v[200001];
int index_tree[200001][2];
ll tree[1000000];
ll depth[200001];
void tree_building(int r){
index_tree[r][0] = ++NodeNum;
for(int i:v[r]) if(depth[i] == 0) {
depth[i] = depth[r] + 1;
tree_building(i);
}
index_tree[r][1] = NodeNum;
}
void update(int d, int l, int r, int x){
if(x < l || r < x) return ;
tree[d]++;
if(l == r) return ;
update(2*d, l, (l+r)/2, x);
update(2*d+1, (l+r)/2 + 1, r, x);
}
ll find(int d, int l, int r, int x, int y){
if(y < l || r < x) return 0;
if(x <= l && r <= y) return tree[d];
return find(2*d, l, (l+r)/2, x, y) + find(2*d+1, (l+r)/2+1, r, x, y);
}
int main(void){
memset(tree, 0, sizeof(tree));
memset(depth, 0,sizeof(depth));
scanf("%d %d", &N, &C);
for(int i=0; i<N-1; i++){
int s,e; scanf("%d %d", &s, &e);
v[s].push_back(e); v[e].push_back(s);
}
int k; scanf("%d", &k); depth[C] = 1;
tree_building(C);
for(int i=0; i<k; i++){
int a, b; scanf("%d %d", &a, &b);
if(a==1){
update(1,1,N,index_tree[b][0]);
}else{
printf("%lld\n", find(1, 1, N, index_tree[b][0], index_tree[b][1]) * depth[b]);
}
}
return 0;
}
