문제링크
문제
N(1 ≤ N ≤ 100,000)개의 정수들이 있을 때, a번째 정수부터 b번째 정수까지 중에서 제일 작은 정수를 찾는 것은 어려운 일이 아니다. 하지만 이와 같은 a, b의 쌍이 M(1 ≤ M ≤ 100,000)개 주어졌을 때는 어려운 문제가 된다. 이 문제를 해결해 보자.
여기서 a번째라는 것은 입력되는 순서로 a번째라는 이야기이다. 예를 들어 a=1, b=3이라면 입력된 순서대로 1번, 2번, 3번 정수 중에서 최솟값을 찾아야 한다. 각각의 정수들은 1이상 1,000,000,000이하의 값을 갖는다.
입력
첫째 줄에 N, M이 주어진다. 다음 N개의 줄에는 N개의 정수가 주어진다. 다음 M개의 줄에는 a, b의 쌍이 주어진다.
풀이 유형
풀이
해당 문제를 풀기 위해서는 세그먼트 트리에 대하여 알아야 한다. 세그먼트 트리는 생각보다 매우 간단한 자료구조다. 그림으로 설명해보겠다.
여기 아래와 같은 수열이 있다.
1
arr = [7,8,6,5,3,9,11,1,2,9,3,8,1,0,5,6]
해당 배열의 숫자들을 포화이진트리의 리프 노드에 채운다. 만약 수의 개수가 2의 거듭제곱수가 아닐 경우 완전이진트리를 이용하여 하는 방법도 있지만, 빠른 이해를 위해 포화이진트리를 예시로 들겠다. 만약, 개수가 2의 거듭제곱수가 아닐 경우 MAX값으로 채워놓도록 하자. 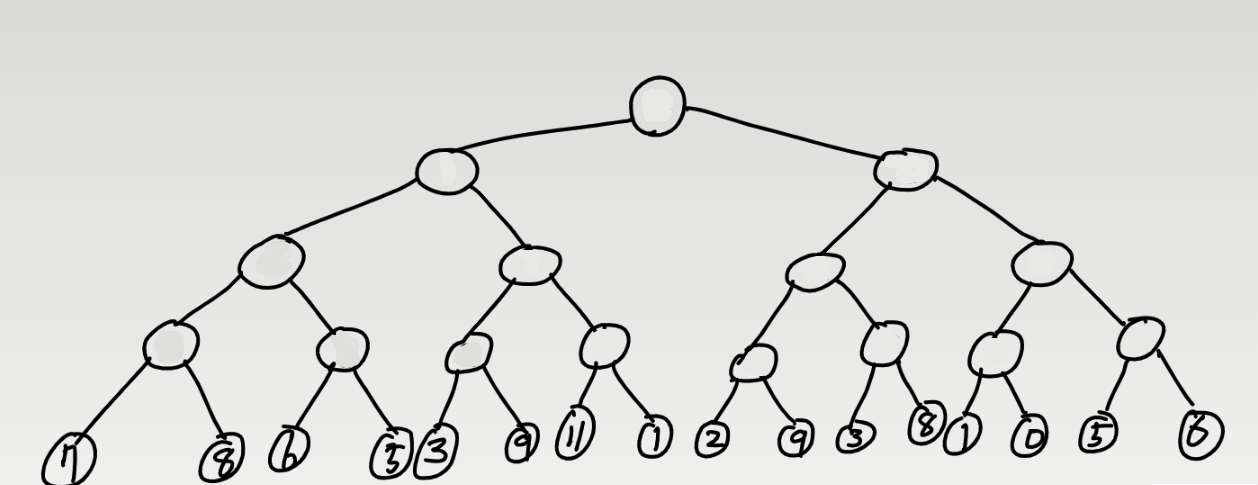
이제 우리는 부모노드를 채워주어야 한다. 부모노드는 자식 노드 중 작은 수의 데이터를 본 노드의 데이터로 삼는다.
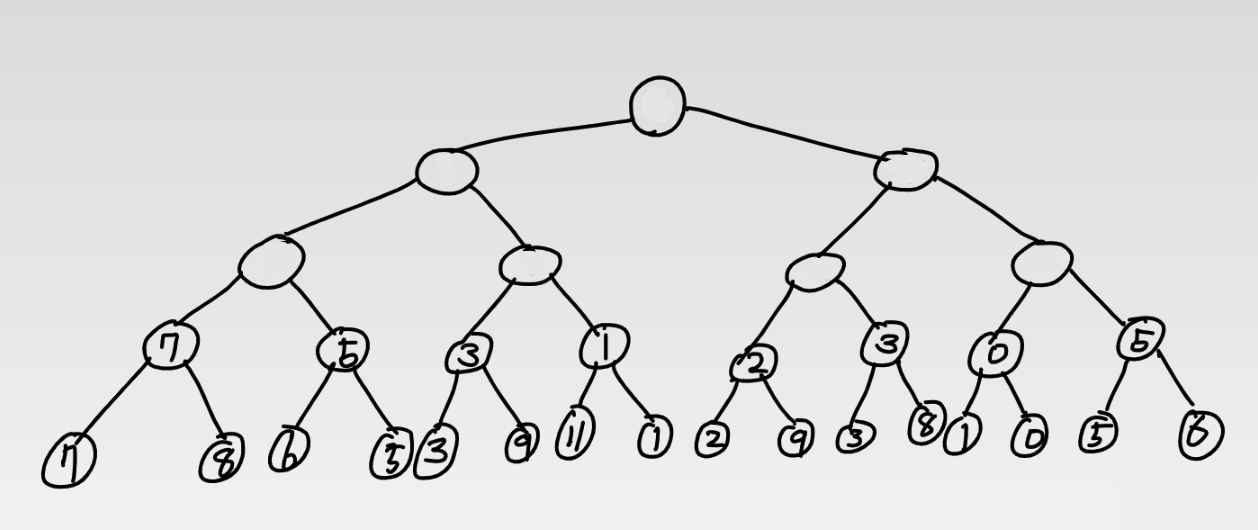
이와 같은 방식으로 위로 위로 트리를 키워 간다.
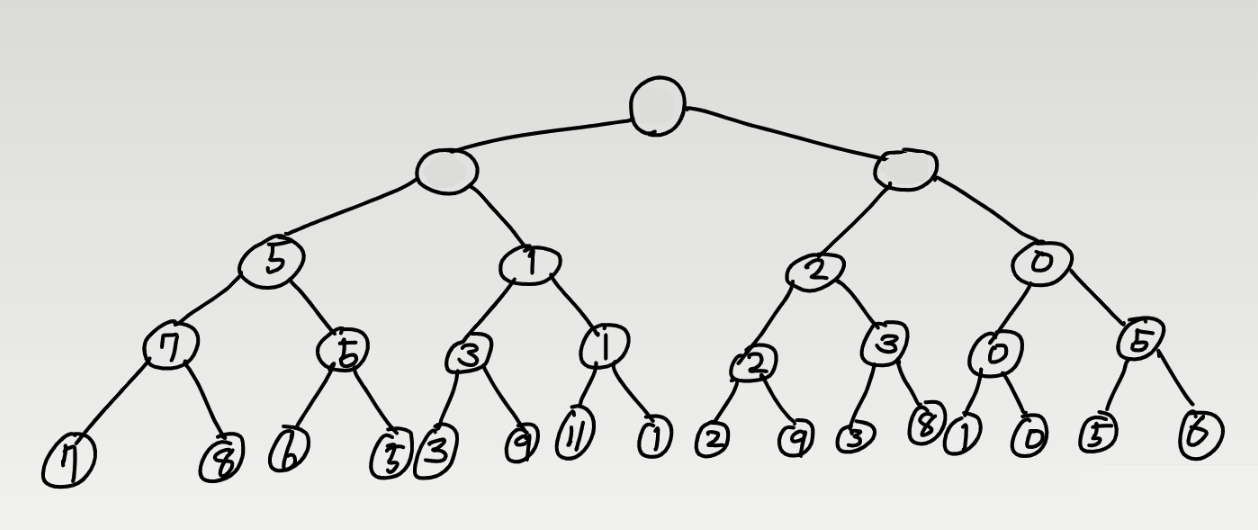
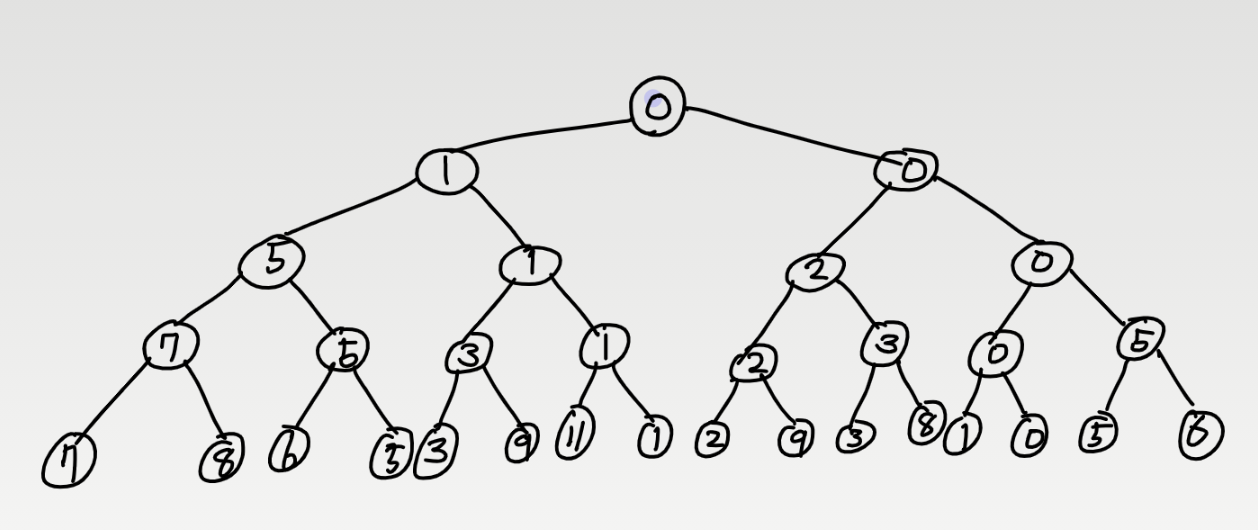
세그먼트 트리가 완성되었다. 트리빌딩을 하는데에는 O(n)의 시간이 소요 된다. 코드로 한 번 보자.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
void tree_building(){
for(int i=0; i < len; i++){ // 리프 노드 채우기
tree[i+len-1].data = num[i];
tree[i+len-1].lll = i;
tree[i+len-1].rll = i;
}
for(int i=len-2; i>=0 ; i--){ // 리프노드에서 시작해서 부모노드 채우기
int l = (i+1) * 2 -1;
int r = (i+1) * 2;
tree[i].data = min(tree[l].data, tree[r].data);
tree[i].lll = tree[l].lll;
tree[i].rll = tree[r].rll;
}
}
정확히는 2*n번 만큼 순회한다. 트리 빌딩에 소요되는 시간은 O(2n) = O(n)이다.
이제는 해당 문제가 어려워진 이유, ‘쿼리’를 처리해줄 차례다. 잘보면 트리 빌딩 단계에서 lll과 rll이라는 변수가 보일 것이다. lll(Left Limit Line), rll(Right Limit Line)으로 해당 노드의 자식 노드가 갖는 범위를 의미한다. 당연히 왼쪽 자식의 시작점, 오른쪽 자식의 끝점이 부모 노드의 시작점과 끝점이 될 것이다.
이제 쿼리문을 처리해줄 차례다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int tree_find(int a, int b, int n){
if(tree[n].lll == a && tree[n].rll == b){
return tree[n].data;
} // 시작점과 끝점이 같다면, 해당 노드의 데이터를 반환한다.
int l = (n+1)*2-1;
int r = (n+1)*2;
if(a > tree[l].rll){
return tree_find(a,b,r); // 범위 자체가 오른쪽 자식에 포함된다면 오른쪽 자식으로 순회한다.
}else if(b < tree[r].lll){
return tree_find(a,b,l); // 범위 자체가 왼쪽 자식에 포함된다면 왼쪽 자식으로 순회한다.
}
else{ //왼쪽 자식과 오른쪽 자식의 범위에 걸쳐 있는 경우
int lret = tree_find(a, tree[l].rll, l);
int rret = tree_find(tree[r].lll, b, r);
return min(lret, rret); // 각각 구해 더 작은 것을 취한다.
}
}
조금만 생각해보면 쉽게 이해할 수 있는 코드다. 찾고자하는 범위가 어느쪽 자식의 범위에 포함되는지를 고려해야한다. 그럴 경우 나올 수 있는 경우의 수는 세가지다.
1
2
3
1. 왼쪽 자식의 범위에 전체 범위가 포함되는 경우.
2. 오른쪽 자식의 범위에 전체 범위가 포함되는 경우.
3. 걸쳐 있는 경우.
각각 경우에 맞게 분기시켜 재귀함수로 노드들을 순회해주면 O(log n)의 시간에 원하는 답을 찾아낼 수 있다.
마무리
그렇게 어렵지 않은 개념이다. 사실 말하자면 dp와도 비슷한 풀이다. 메모이제이션을 통해, 우리는 답을 쉽게 알 수 있다. 세그먼트 트리를 이용해야하는 문제들은 심심치 않게 나온다. 구간합 구하기 문제가 대표적인 예시다. 해당 문제에서는 단순히 작은 값만을 부모 노드의 값으로 삼았다면, 구간합 구하기의 경우 자식의 합을 노드의 값으로 삼는다. 조금 더 나아가면 ‘늦은 전파’를 이용하는 세그먼트 트리 문제도 있는데, 나중에 기회가 되면 다뤄볼 예정이다.
코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>
#include <queue>
#include <cstring>
#include <vector>
#include <algorithm>
#include <stack>
#include <map>
#include <cmath>
#define Min(X, Y) ((X) < (Y) ? (X) : (Y))
#define Max(X, Y) ((X) > (Y) ? (X) : (Y))
using namespace std;
class Node{
public:
int data;
int lll;
int rll;
};
int N, M;
int num[200001];
int len;
Node tree[300001];
int length(int n){
int ret = 1;
while(ret < n) ret *= 2;
return ret;
}
void tree_building(){
for(int i=0; i < len; i++){
tree[i+len-1].data = num[i];
tree[i+len-1].lll = i;
tree[i+len-1].rll = i;
}
for(int i=len-2; i>=0 ; i--){
int l = (i+1) * 2 -1;
int r = (i+1) * 2;
tree[i].data = min(tree[l].data, tree[r].data);
tree[i].lll = tree[l].lll;
tree[i].rll = tree[r].rll;
}
}
int tree_find(int a, int b, int n){
if(tree[n].lll == a && tree[n].rll == b){
return tree[n].data;
}
int l = (n+1)*2-1;
int r = (n+1)*2;
if(a > tree[l].rll){
return tree_find(a,b,r);
}else if(b < tree[r].lll){
return tree_find(a,b,l);
}
else{
int lret = tree_find(a, tree[l].rll, l);
int rret = tree_find(tree[r].lll, b, r);
return min(lret, rret);
}
}
int main(void){
scanf("%d %d", &N, &M);
memset(num,111,sizeof(num));
len = length(N);
for(int i=0; i<N; i++){
int n; scanf("%d",&n);
num[i] = n;
}
tree_building();
for(int i=0; i<M; i++){
int n, m; scanf("%d %d", &n, &m); n--; m--;
int anw = tree_find(n,m,0);
printf("%d\n",anw);
}
}
